Weijiu Liu (ÁõÍþ¾Å)

Department of Mathematics
University of Central Arkansas
201 Donaghey Avenue
Conway, AR 72035, USA
TEL (501) 450-5684
FAX (501) 450-5662
E-Mail: weijiul@uca.edu

o    Feedback control of the blood glucose system

o    Feedback control of the intracellular calcium system in yeast cells

o    Feedback control of the intracellular calcium system in non-excitable cells

o    Feedback control of the intracellular sterol system in yeast cells

Preface

Mathematical control theory of applied partial differential equations is built on linear and nonlinear functional analysis and many existence theorems in control theory result from applications of theorems in functional analysis. This makes control theory inaccessible to students who do not have a background in functional analysis.

 

Many advanced control theory books on infinite-dimensional systems were written, using functional analysis and semigroup theory, and control theory was presented in an abstract setting. This motivates me to write this text for control theory classes in the way to present control theory by concrete examples and try to minimize the use of functional analysis. Functional analysis is not assumed and any analysis included here is elementary, using calculus such as integration by parts. The material presented in this text is just a simplification of the material from the existing advanced control books. Thus this text is accessible to senior undergraduate students and first-year graduate students in applied mathematics, who have taken linear algebra and ordinary and partial differential equations.

 

Elementary functional analysis is presented in Chapter 2. This material is required to present the control theory of partial differential equations. Since many control concepts and theories for partial differential equations are transplanted from finite-dimensional control systems, a brief introduction to feedback control of these systems is presented in Chapter 3. The topics covered in this chapter include controllability, observability, stabilizability, pole placement, and quadratic optimal control. Theories about the feedback stabilization of linear reaction-convection-diffusion equations are presented in Chapter 4. Both interior and boundary control problems are addressed. The methods employed to handle the problems include eigenfunction expansions, integral transforms, and optimal control. Finally, theories about feedback stabilization of linear wave equations are presented in Chapters 5 and 6. First, the one-dimensional wave equations are considered, then higher dimensional wave equations follows, since it is easier to use the one-dimensional equations to illustrate the theories and methods. The perturbed energy method is emphasized to deal with both interior and boundary control problems while the optimal control technique is used.

 

This text can be used as a textbook for an introductory one-semester graduate course on control theory of partial differential equations. If students do not have a background in finite-dimensional control systems, one can cover Sections 3.1-3.7 of Chapter 3, Sections 4.1-4.3 of Chapter 4, all sections of Chapter 5, and Sections 6.1-6.3 of Chapter 6. Material from Chapter 2 can be introduced whenever needed, and all material about optimal control can be skipped. If students have had a background in both functional analysis and finite-dimensional control systems, one can cover all of Chapters 4, 5, 6 and give a brief review of Chapters 2 and 3.

 

Inevitably, the material is selected from the topics I have worked on or am most familiar with, and many other important topics are not covered. Control theory for other applied partial differential equations, such as elastic equations, thermoelastic equations, viscoelastic equations, Schr¨odinger’s equations, and Navier-Stokes equations, is not included. In addition, exact and approximate controllability is not discussed since it is difficult to present it in an elementary way.

 

I thank my PhD advisor, Dr. Graham H. Williams, for introducing me to the area of control theory of partial differential equations. I thank Drs. George Haller, Mirsolav Krstic, and Enrique Zuazua for having directed my research and providing stimulating feedback on my work. I thank two reviewers for their hard, serious work of reading and evaluating this text and giving constructive suggestions. I thank my students, such as Jingvoon Chen, for using this text and correcting mistakes. I thank Ms. Peggy Arrigo and Dr. Danny Arrigo for their language-editing. Finally, I thank my family for their constant support.

In general terms, control theory is a separate branch of mathematics and can be described as the study of how to design the process of influencing the behavior of a physical system to achieve a desired goal. Control theory consists of three main components: feedback control, controllability, and optimal control. My research interest  focuses on feedback control because, in comparison with controllability and optimal control, it is mathematically simpler and physically more applicable in solving control problems in engineering and sciences.

Feedback control  refers to an operation that, in the presence of disturbance, tends to reduce the difference between the output of a system and some reference output and does so on the basis of this difference.

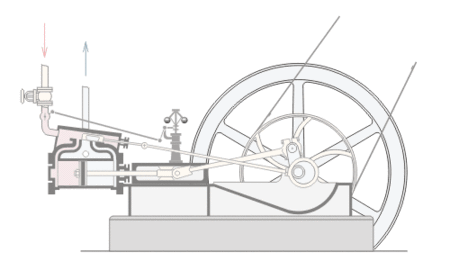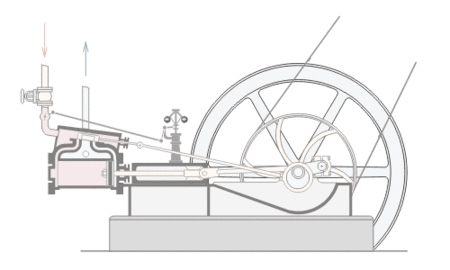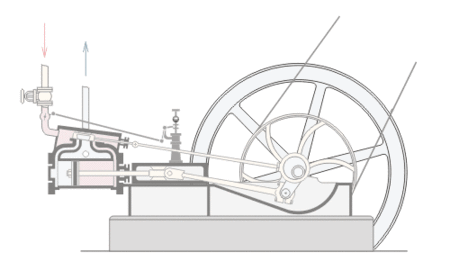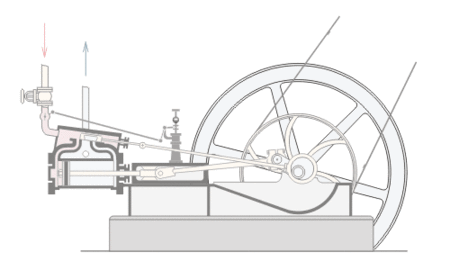
Feedback control theory has developed an extensive literature covering its various concepts, theories, and applications. Significant works in the early stage of feedback control were due to Watt, Minorsky, Hazen, and Nyquist, among many others. The first significant work in automatic control was James Watt's centrifugal governor for the speed control of a steam engine in the eighteenth century.

In the 1930s, automatic control was still an engineer's dominion. Feedback controllers were designed and used by process engineers to regulate temperatures and pressures, by mechanical engineers to control the speed of engines, and by telephone engineers to build linear amplifiers. Despite their wide use, a large fraction of feedback control design consisted of ``trial and error" methods with little analysis involved if any at all. In 1934, Ivanoff  stated that ``the science of the automatic regulation of temperature is at present in the anomalous position of having erected a vast practical edifice on negligible theoretical foundations."

While feedback controllers were generally specialized mechanisms designed to solve immediate industrial problems, there were also a small number of researchers examining the theory behind these controllers. In the 1920s, while studying the automatic steering of ships at sea, Nicolas Minorsky used differential equations to model the dynamics of the ship and proportional-integral-derivative (PID) controllers and then investigated their stability. In the 1930s, using open-loop responses to steady-state sinusoidal inputs, Harry Nyquist developed a theory about the stability of closed-loop systems. Harold Hazen introduced the term servomechanisms for position control systems with a changing input and designed relay servomechanisms to track the changing input. During the decade of the 1940s, frequency-response methods represented by the Bode diagram method due to Hendrick Bode were developed. From the end of the 1940s to the early 1950s, the root-locus method due to Walter R. Evans was established. The frequency-response and root-locus methods made it possible for engineers to design linear single-input-single-output closed-loop control systems that satisfy a set of performance requirements. These early development of control theory constitutes classical control theory with the frequency-response and root-locus
methods as its core.

Modern feedback control systems have becomes more and more complex. These systems have many inputs and outputs. The stringent requirements on accuracy lead to distributed parameter systems in which partial differential equations is required to model the physical systems. Therefore classical control theory, which deals only with single-input-single-output control systems, becomes powerless for the modern complex control systems. Since about 1960, modern control theory has been developed to cope with the increasing complexity of multiple-inputs-multiple-outputs control systems. Unlike classical control theory that is based on frequency-domain analysis, modern control theory is based on time-domain analysis and synthesis using state variables.

Since the 1960s, control theory of distributed parameter systems has followed right on the heels of that of finite dimensional dynamical systems, but with slower and heavier tread. Many control concepts and theories in finite dimensional systems have been transplanted to distributed parameter systems. Control theory for many distributed parameter systems, such as the wave equation, reaction-convection-diffusion equations, elastic equations, thermoelastic equations, viscoelastic equations, Schrödinger's equations,  and Navier-Stokes equations, has been well developed.

Recently it has become appreciated that control theory can be used to analyze non-engineering systems, such as biological systems and control theory has been inspired by these biological systems.