My dissertation research applies
computational design optimization techniques, that are commonly used in the
aerospace industry, to the design of open channel flows. In order to understand
the numerical model and the characteristics of various channels, I modeled many
different channels, using HIVEL2D.
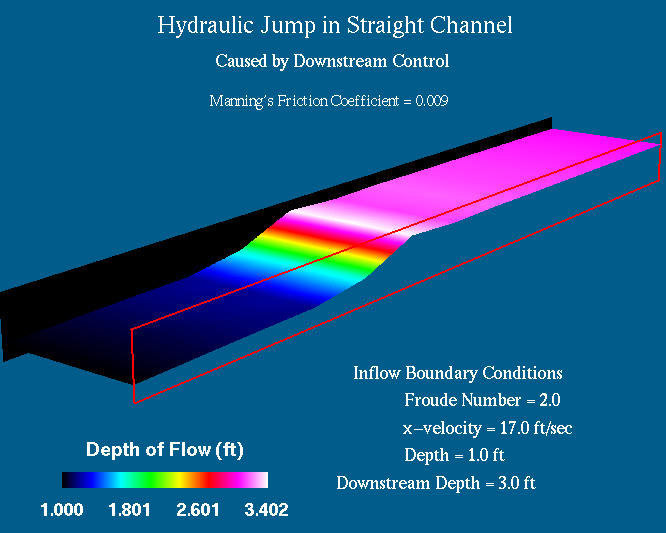
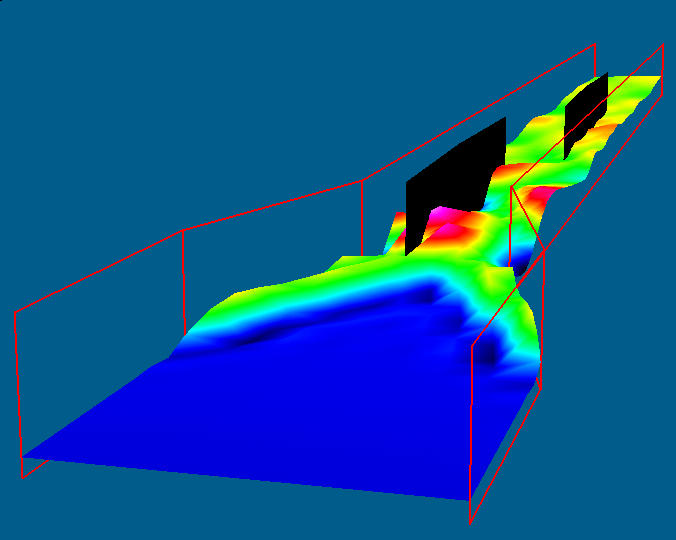
We are using the 2D, depth-averaged,
viscous, shallow water equations. HIVEL2D is the code that
numerically solves these equations for a given grid and was written by Dr.
Charlie Berger at the Waterways
Experiment Station . These equations make certain assumptions, such as no
vertical velocity, mild slope assumptions, and hydrostatic pressure
distribution. In the design process, the key to success is the cancellation of
the series of hydraulic jumps that are developed. But at a hydraulic jump, the
assumptions of no vertical velocity and of a hydrostatic pressure distribution
are violated, technically rendering the shallow water equations invalid in this
region. Recognizing this limit to the computational design process, we are
still able to identify the influential design parameters. It may be necessary,
in future research, to use a different set of 2D equations or to use the full
3D equations with a free surface model.

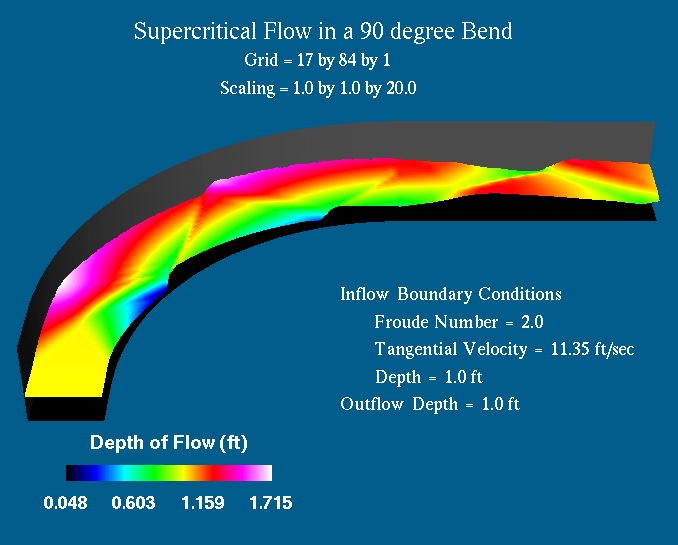
Since computational design procedures have
not been previously applied to open channel flow, one aspect of my research is
to recast the problem into an optimization problem. In particular, I am
interested in determining the best objective function to minimize. This
objective function should be quite sensitive to changes in the design variables
and should attain its minimum for a physically realistic optimum flow. Currently,
I am studying an objective function that attains its minimum for flow with a
constant depth. Unfortunately, for a viscous flow, the form of the shallow
water equations that we are using does not allow a constant depth across the
channel.
For more information, please read the
following:
“An Efficient, Robust Design Tool for
Open-Channel Flow”, ASCE J. Hydraulic Eng, Junary, 2001, pp. 62-70.



