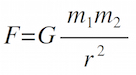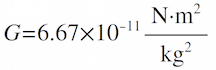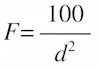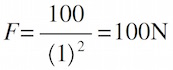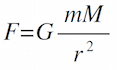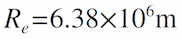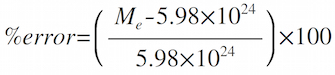PHYS 1401: Descriptive Astronomy

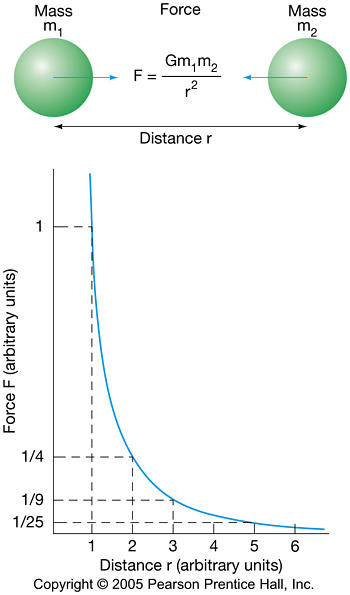
Introduction

It's a common anecdote, the one about Newton figuring out gravity when he saw an apple fall from a tree. The apple may or may not have hit him on the head, but it is true that Newton was able to figure out why the apple fell, as well as why the planets stay in their orbits. The idea of an action-at-a-distance force (as opposed to a contact force) was a significant scientific advancement.

In most situations Newton's Law of Gravitation (action at a distance) is sufficient. Only in cases of very large gravitational fields or when extremely high precision is needed does Newtonian gravity start to give incorrect results. In this lab you will be applying Newton's Law of Gravitation:

where F = gravitational force between objects 1 and 2,
G = universal gravitational constant:

m₁, m₂ = masses of objects 1 and 2, and
r = separation of masses, measured center to center.

Objectives

• Examine inverse-square behavior
• Practice using Newton's Law of Gravitation to solve quantitative problems
• Describe the force behavior qualitatively
• Use Newtonian gravity to determine the mass of the earth

The Inverse−Square Force Behavior

The gravitation equation can be rewritten in a simpler form, provided we are very careful to use the proper set of units:

where F = gravitational force (in units of Newtons (N)) between a 10kg mass and Earth, and
d = separation of masses, measured in units of Earth radii (R_e = 1 Earth radius).

Note carefully that this equation refers specifically and only to the force on a 10kg mass due to the Earth. It is not valid for any other size mass or any other planet!

Using this relationship, the gravitational force on the 10kg mass at 1 R_e (on the surface of the Earth) would be:

Questions

1. Construct a table: Use the table shown below as an example to make a similar table in your lab notebook to examine what happens to the force as we change the distance between the 10kg mass and the Earth.

d (Re)	F (N)	d (Re)	F (N)
1		20
2		30
4		40
10		50

2. Calculate and compare: Compare the size of the force when d = 1 to the force when d = 2. Calculate the ratio F₁/F₂. Now compare the force at d = 4 to d = 2, and calculate the ratio F₂/F₄. Think about ratios: While the force values are calculated specifically for that 10kg mass, do the ratios you calculated depend on the mass being 10kg? Comment on this!
3. Zero force? At the distances you calculated, did this 10 kg mass ever have exactly zero gravitational force acting on it due to the Earth?
4. Zero where? What distance from the Earth to the mass would be required for the mass to have exactly zero gravitational force on it due to the Earth?
5. Weightlessness? What condition(s) is necessary for the mass to be weightless, even if there is a gravitational force pulling on it?
6. Shrink the Earth: Now imagine the Earth crushed down to the size of a marble, with no change in its mass. What would the gravitational force on the 10 kg mass be if it was located at a distance d = 10⁻²R_e?

The following questions are mental puzzles about gravitation. To solve them you will need to apply the concepts of Newtonian gravity. You can always choose to support your arguments mathematically, but you should use words/pictures to make sure you grasp the concepts.

8. Suppose the radius of the Sun suddenly shrank to a tenth of its present size, with no change in mass. What would happen to the force on the Earth due to the Sun?
9. Imagine changing the Earth from a solid sphere to a spherical shell having the same radius and mass. How would this change the weight of a mass
   1. on the surface of the Earth?
   2. 10 Earth-radii (d = 10) away?
   3. inside the Earth?

10. Imagine a hole in the smooth airless Earth bored from one side, passing straight through the center of the Earth, and coming out the opposite side. Drop a baseball down this hole, releasing it from one meter above the surface. What would be the velocity and acceleration of the ball
    1. at the start,
    2. at the center,
    3. when it comes out the other side. Will the resulting motion be periodic?

Gravity and Astrology

It looks all technical and official, but it's not science. Not even a little bit.

Just for fun, let's do a little calculation. Let's say a baby is born when Mars is at opposition. Let's go ahead and calculate the gravitational force on that baby, then let's compare it to the gravitational force exerted on the child by the doctor performing the delivery, and see which one would have the greater influence. Use:

where G = universal gravitational constant:

m = 3 kg = the mass of the baby,
M = either the mass of Mars or the obstetrician, and
r = the separation between the baby and either Mars or the doctor at the instant of birth.

Questions

11. Force due to Mars: Calculate F₁, the force on the baby due to Mars. Mars has a mass M₁ = 6.23×10²³kg, and when it is at opposition, it is at a distance r₁ = 3.78×10¹¹m.
12. Force due to doctor: Calculate F₂, the force on the baby due to the doctor. A reasonable mass would be M₂ = 65 kg, and the distance would be small, r₂ = 1m.
13. Which is greater? What has a greater gravitational influence on the infant, the presence of Mars or the presence of the doctor?

Calculating the Mass of the Earth

The weight of an object is literally the measurement of the gravitational force exerted on it by the Earth. If you know how much an object weighs, you know the force on it. Newton's Third Law of Motion tells us that we also know exactly how much force is being exerted on the Earth by the object as well!

Rearrange Newton's Law of Gravity, solving the equation for the Mass of the Earth:

where M_e = mass of the Earth,
F = gravitational force between the object and Earth,
R_e = separation of masses = radius of the Earth:

G = universal gravitational constant:

m = mass of the object attracted to the Earth.

Procedure and Questions

14. Weigh: Using a scale that measures force in Newtons (N), weigh an object with a known mass.
15. Record: both the mass (M) and the weight (F) of the object.
16. Calculate: the mass of the Earth (M_e) using the above equation.
17. How accurate is your result? The accepted value for the mass of the Earth is M_e = 5.98×10²⁴kg. Calculate the percent error in your value: