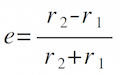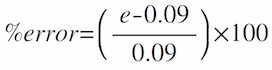Introduction
Back in 1609, Johannes Kepler did not have a computerized planetarium that he could use to visualize the solar system at whatever instant he chose. What he did have was an enormous quantity of data inherited from Tycho Brahe, an observational astronomer so careful and meticulous that his data can still be used today to locate astronomical objects. Tycho had hoped that Kepler would be able to use his data to prove mathematically the correctness of his own geocentric cosmology (a complicated variation of Ptolemy's model). What happened instead was that Kepler went where the data took him, and it wasn't in Tycho's direction.
Kepler's First Law states that planets orbit the sun, and the orbits are ellipses. We are going to take a very small portion of data similar to what was available to Kepler, and determine the orbit of Mars using the method that he used.
Kepler was able to determine the orbital period of Mars (with respect to the stars). He determined that Mars orbited the Sun once every approximately 687 days. This is important since this tells us that Mars will be at the same location in its orbit every 687 days. Why is this important? Tycho's accurate data for Mars in the sky provided its direction but not its distance. But one can triangulate the distance by observing Mars in the same position 687 days apart.
Objectives
- Apply geometric methods of triangulation
- Use observational data to construct the orbit of the planet Mars
- Demonstrate Kepler's First Law of Planetary Motion
- Label and define the properties of an ellipse
- Apply the properties of ellipses to the orbit to determine the eccentricity e of Mars' orbit
- Calculate the percent error in your value of e
Constructing an Orbit
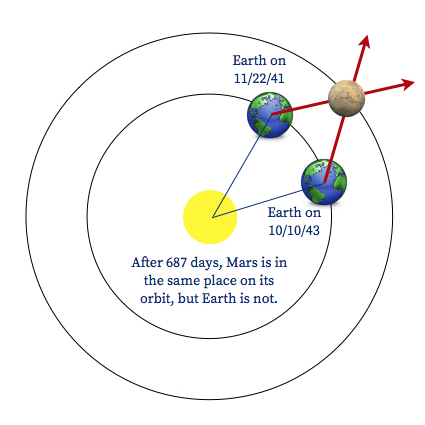
To find where Mars is with respect to the sun, we need to know both where the Earth is with respect to the sun, and then where Mars is with respect to the Earth. The figure above illustrates this.
Each data pair on the table below represents a pair of observations of Mars, taken from here on Earth. In each case, the observations are separated in time by exactly 687 days, or the length of one Martian year. Thus, each pair of observations puts Mars in the same place on its orbit relative to the sun. However, that does not put it in the same place relative to the Earth. This is because the Earth is also moving with respect to the sun, and after 687 days, the Earth is definitely not back in the same place it started.
The heliocentric longitude of Earth is the position of the Earth relative to the sun, and the geocentric longitude of Mars is the position of Mars relative to the Earth. Use the following table of observations to construct the orbit of the planet Mars:
Date |
Heliocentric Longitude of Earth |
Geocentric Longitude of Mars |
1 |
March 21, 1931 |
180° |
118° |
| February 5, 1933 |
136° |
168° |
2 |
April 20, 1933 |
210° |
151° |
| March 8, 1935 |
167° |
204°
|
3 |
May 26, 1935 |
245° |
187° |
| April 12, 1937 |
202° |
246°
|
4 |
September 26, 1939 |
3° |
301° |
| August 13, 1941 |
320° |
20° |
5 |
November 22, 1941 |
60° |
12° |
| October 10, 1943 |
17° |
80° |
6 |
January 21, 1944 |
121° |
66° |
| December 8, 1945 |
76° |
123° |
7 |
March 19, 1946 |
178° |
108° |
| February 4, 1948 |
135° |
153° |
8 |
April 4, 1948 |
195° |
138° |
| February 20, 1950 |
152° |
191° |
- Construct the orbit of the Earth: Start by assuming that the Earth's orbit is circular. Use a compass to draw a circle with a radius of 10 squares of your grid paper. This sets the scale of your orbit to 1 square = 0.10 AU.
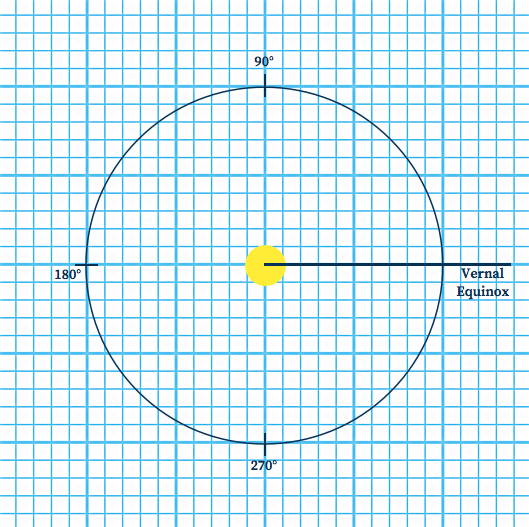
- Draw a reference line: As shown above, draw a horizontal line from the sun and label it "Vernal Equinox." This represents 0°, and we will measure all angles with respect to this guideline.
|
|
- Locate the position of the Earth: Use the protractor to measure the angle of the heliocentric longitude of the Earth with respect to the Vernal Equinox. Place a dot at the location, then use this as your reference to locate the position of Mars.
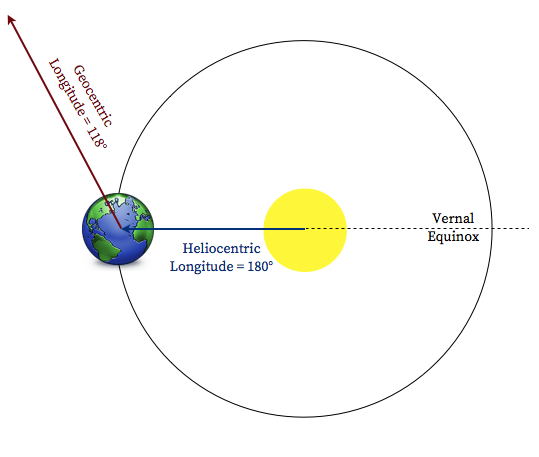
- Measure the geocentric longitude of Mars: From the dot of the Earth, use the protractor to measure this angle with respect to a horizontal reference parallel to the Vernal Equinox. Using a ruler, draw the line of sight as shown above.
Repeat for the second observation of the data pair: The intersection of the two geocentric longitude lines of sight locates the planet Mars for that pair of observations. Do this for each pair of observations, until you have plotted all eight locations of Mars.
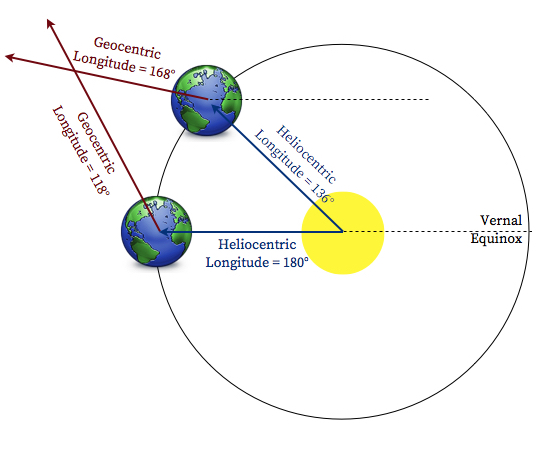
- Construct the orbit: Draw a smooth curve through the eight points of the orbit of Mars (do not connect the dots).
Analyzing the Orbit
- Is it a perfect circle? Apply the definitions and properties of an ellipse to your orbit using the example shown below.
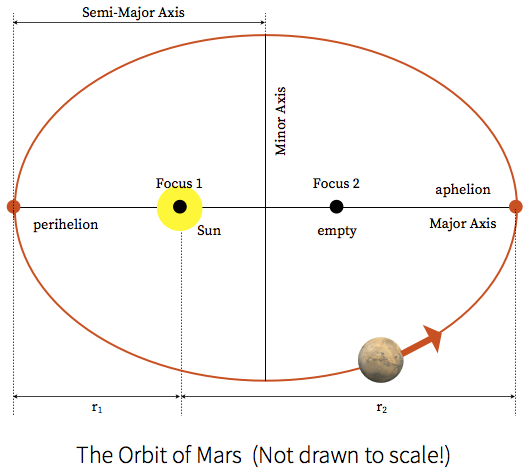
- Locate perihelion: Find the data point closest to the origin (Sun) and label it "Near Perihelion." Because you have only eight points on the orbit, you cannot be certain that the point you plotted is the actual point of perihelion, so label it as "near."
- Locate aphelion: Find the data point furthest from the origin (Sun) and label it "Near Aphelion."
- Draw the major axis: Draw a single line that passes through the Sun with ends on the Martian orbit and close to the near perihelion and near aphelion points. This line does not have to pass through any specific data point. Label the line the Major Axis.
- Calculate the distance: Measure the length of the Major Axis. Divide this value by two; this is the length of the Semi-Major Axis. What is the length of the Semi-Major Axis in AUs? What, then, is the average distance from the Sun to the planet Mars?
- Find the center: Now you should be able to locate and label the center of the Martian orbit. Where is the Sun relative to the center of the orbit?
- Calculate the eccentricity: For the ellipse you have just drawn, label the distance from the sun to perihelion r1. Measure this distance. Label and measure the distance from the sun to aphelion, and call it r2. Use these values to calculate the eccentricity:
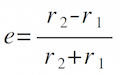
- Determine the accuracy: The known eccentricity of Mars' orbit is e = 0.09. How close is your value? Calculate the percent error in your result:
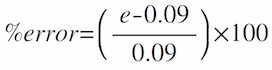
|